3 5 Pratice Continued for K Working With Sets
PRATICE PROBLEMS ON COMPLEMENT OF A SET
(1) If U = {x : 0 ≤ x ≤ 10, x ∈ W} and A = {x : x is a multiple of 3}. Find A'.
(2) If U is the set of all natural numbers and A' is the set of all composite numbers, then what is A?
(3) If U = {a, b, c, d, e, f, g, h}, A = {a, b, c, d} and B = { b, d, f, g}, find
(i) A∪B (ii) (A∪B)' (iii) A∩B (iv) (A∩B)'
(4) If U = { x : 1 ≤ x ≤ 10, x∈ℕ}, A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 9, 10}, find
(i) A' (ii) B' (iii) A'∪B' (iv) A'∩B'
(5) If U = {0, 1, 2, 3, 4, 5, 6, 7} and E = {2, 3, 5, 7}, list the set E' and illustrate E and E' on a Venn diagram.
Hence find :
(a) n(E) (b) n(E') (c) n(U)
(6) Consider U = {x | x ≤ 12, x∊ Z+}
A = {2, 7, 9, 10, 11} and B = {1, 2, 9, 11, 12}.
a) Show these sets on a Venn diagram.
b) List the elements of :
(i) A n B (ii) A U B (iii) B' (iv) A'
(7) Simplify:
(a) AUA' for any set A∈ U.
(b) A n A' for any set A∈ U.
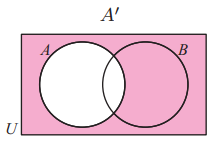
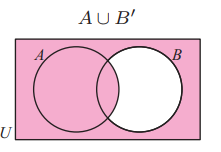
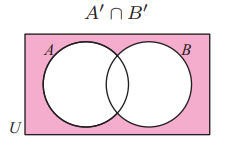
(8)If A and B are two non-disjoint sets, shade the region of a Venn diagram representing:
(a) A' (b) A' n B (c) A U B' (d) A' n B'

(1) Solution :
First let us write the given sets.
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {3, 6, 9}
So, A' is the set of all elements in U which are not in A.
A' = {0, 1, 2, 4, 5, 7, 8, 10}
(2) Solution :
Let U = {1, 2, 3, 4, 5, .................}
Set U is containing the set of natural numbers, including prime and composite numbers.
A' is containing composite numbers, then the set A will contain set of prime numbers.
(3) Solution :
U = {a, b, c, d, e, f, g, h}, A = {a, b, c, d} and B = { b, d, f, g}
(i) A∪B = {a, b, c, d} ∪ { b, d, f, g}
A∪B = {a, b, c, d, f, g}
(ii) Write the elements from U (universal set) by excluding the elements from AUB.
(A∪B)' = {e, h}
(iii) Write the common elements of the sets A and B.
A∩B = {b, d}
(iv) Write the elements from U (universal set) by excluding the elements from AnB.
(A∩B)' = {a, c, e, f, g, h}
(4) Solution :
U = { x : 1 ≤ x ≤ 10, x∈ℕ}, A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 9, 10}
First we will write the given sets A and B.
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 5, 7, 9}
B = {2, 3, 5, 9, 10}
(i) A' = {2, 4, 6, 8, 10}
(ii) B' = {1, 4, 6, 7, 8}
(iii) A'∪B' = {2, 4, 6, 8, 10} ∪ {1, 4, 6, 7, 8}
A'∪B' = {1, 2, 4, 6, 7, 8, 10}
(iv) A'∩B' = {2, 4, 6, 8, 10} ∩ {1, 4, 6, 7, 8}
A'∩B' = {4, 6, 8}
(5) Solution :
U = {0, 1, 2, 3, 4, 5, 6, 7} and E = {2, 3, 5, 7}
E' = {0, 1, 4, 6}
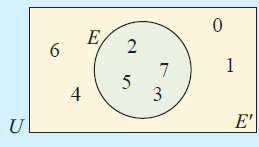
(a) n(E) = 4 (Number of elements in the set E)
(b) n(E') = 4 (number of elements other than E)
(c) n(U) = 8 (Number of elements in all sets)
(6) Solution :
U = {x | x ≤ 12, x∊ Z+}
Z is a set of integers.
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, A = {2, 7, 9, 10, 11} and B = {1, 2, 9, 11, 12}.
(a)
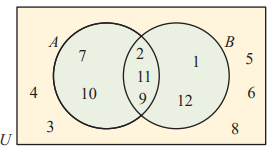
(i) A n B = {2, 9, 11}
(ii) A U B = {1, 2, 7, 9, 10, 12}
(iii) B' = {3, 4, 5, 6, 7, 8, 10}
(iv) A' = {1, 3, 4, 5, 6, 8, 12}
(7) Solution :
(a) AUA' for any set A∈ U.
Let U = {1, 2, 3} A = {1}
So, A' = {2, 3}
AUA' = {1, 2, 3} = U
(b) A n A' for any set A∈ U.
A n A' = {1} n {2, 3}
A n A' = Null set
(8) Solution :
(a) A'
(b) A'nB
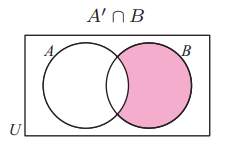
(c) AUB'
(d) A'nB'

Apart from the stuff given above, if you need any other stuff in math , please use our google custom search here.
Kindly mail your feedback tov4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
kellybarigoinathe.blogspot.com
Source: https://www.onlinemath4all.com/practice-problems-on-complement-of-a-set.html
0 Response to "3 5 Pratice Continued for K Working With Sets"
Post a Comment